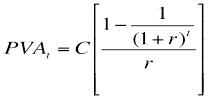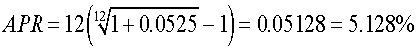The Time Value of Money (“TVM”) is a concept on which the rest of finance theory rests on. Therefore, it is critical that students understand this concept well. We expand on the Time Value of Money under the following headings:
- What does the “Time Value of Money” mean or capture?
- Why does the Value of Money Decline?
- The Present Value Formula
- Infographic on the Time Value of Money
- Computing the Time Value of Money
- Interest Rates and Compounding Frequencies
- Annuities
- Perpetuities
- Interest Rate Conventions
- Continuous Compounding
1) What does the “Time Value of Money” mean or capture?
Most students agree that what $10, today, will buy will be more than what $10 will buy in 5 years in the future. Similarly, they also agree $10 would have got them a lot more 5 years ago than what it will get them today. Since they agree that this is true, I tell them that they have understood the time value of money concept! This is exactly what the time value of money concept in finance is trying to show. As time flows the value of money declines. (Article Index)
2) Why does the Value of Money Decline?
The value of money declines due to the combined impact of the following:
- Inflation in the economy;
- Risks involved in delayed receipts of cash or financial transactions; and
- Opportunity cost of capital delayed.
While each of these forces alone can cause the value of money to decline individually, all the three usually act with different degrees of impact to cause a decline in the value of money as time flows. (Article Index)
3) The Present Value Formula
The present value formula quantifies how fast the value of money declines. This formula shows you how much once single cash payment (FV) received in a future time period (t) is worth in today’s terms (PV).
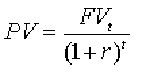
Present Value (PV) stands for the value of the money in today’s terms.
Future Value (FV) stands for the amount of cash received in the future.
r is the discount rate or the speed at which the decline in value is happening (covered in detail later).
t is the time period in which the future value or cash is received. (Article Index)
4) Infographic on the Time Value of Money
The GraduateTutor.com finance team has put together this infographic on the Time Value of Money for the visual learners. We have a follow up infographic on the commonly used Time Value of Money formulas.
Please feel free to embed this infographic using the code below this post. Do provide us credit for this poster by linking to us.

Time Value of Money – An infographic by the finance tutoring team at GraduateTutor.com. (Article Index)
(Content below is contributed by Prof. Alan Anderson)
5) Computing the Time Value of Money
If a sum is invested today, it will earn interest and increase in value over time. The value that the sum grows to is known as its future value. Computing the future value of a sum is known as compounding.
The present value of a sum is the amount that would need to be invested today in order to be worth that sum in the future. Computing the present value of a sum is known as discounting.
The Future Value of a Sum
The future value of a sum depends on the interest rate and the interval of time over which the sum is invested. This is shown with the following formula:
FVt = PV*(1+r)t
where:
FVt = future value of a sum invested for t periods
r = periodic interest rate
PV = present value
t = number of periods until the sum is received
Each period may be a year, a month, a week, etc. The terms in the formula must be consistent with each other; for example, if it is measured in months, then r must be a monthly rate of interest.
As an example, suppose that a sum of $1,000 is invested for four years at an annual rate of interest of 3%. What is the future value of this sum? In this case, t = 4, r = 3% and PV = $1,000.
FVt = PV(1+r)t
FV4 = 1,000(1+.03)4
FV4 = 1,000(1.12551)
FV4 = $1,125.51
The Present Value of a Sum
The formula for computing the present value of a sum is:
Note that the present value is simply the inverse of the future value.
As an example, how much must be deposited in a bank account that pays 5% interest per year in order to be worth $1,000 in three years? In this case, t = 3, r = 5% and FV3 = $1,000.
Present Value Or What must be deposited to get $1,000 = 1,000/(1.1576) = $863.84 (Article Index)
6) Interest Rates and Compounding Frequencies
Compounding refers to the frequency with which interest rates are charged or paid during a given year. In practice, interest rates can be compounded anywhere from once per year to once per day; the theoretical limiting case is known as continuous compounding, in which rates are compounded at every instant in time. Compounding frequency is one of the most important determinants of the future value and the present value of a sum.
For example, if a bank offers a 4% rate of interest with annual compounding, an investor who holds $1,000 in the bank for one year will have a balance of: $1,000(1 + 0.04) = $1,040 at the end of the year. In other words, the future value of this sum is $1,040.
If the interest is compounded semi-annually, then the investor will receive half of the annual rate twice per year; i.e., 2% every six months during the year. At the end of six months, the investor will have a balance of: $1,000(1 + 0.02) = $1,020 at the end of the year, the investor will have a balance of: $1,020(1 + 0.02) = $1,000(1 + 0.02)(1 + 0.02) = $1,000(1 + 0.02)2 = $1,040.40
In this case, since the principal is $1,000, the total interest is $40.40. Of this:
$40 is simple interest (interest on principal)
$0.40 is compound interest (interest on interest)
In this case, the investor received an interest payment of $1,000(0.02) = $20 at the end of six months, for a balance of $1,020. The interest payment at the end of the year was based on the principal ($1,000) and the interest ($20) in the account. The interest paid on the principal was $1,000(0.02) = $20 and the interest paid on the interest was $20(0.02) = $0.40. Combined with the $20 interest paid at the end of six months, the total interest paid during the year was $20 + $20 + $0.40 = $40.40. Of this, the $40 was based on the principal; this is the simple interest. The remaining $0.40 was based on the interest earned during the year; this is the compound interest.
As the compounding frequency increases, the simple interest earned during a given period remains fixed, but the compound interest increases. For example, with quarterly compounding, the investor in the previous example will receive 1% every three months; at the end of the year the investor will have a balance of:
$1,000(1 + 0.01)(1 + 0.01) (1 + 0.01)(1 + 0.01)
= $1,000(1 + 0.01)4 = $1,040.60
In this case, the total interest is $40.60. Of this:
$40 is simple interest (interest on principal)
$0.60 is compound interest (interest on interest)
This demonstrates an important result: as the compounding frequency increases, the future value of a sum increases.
As another example, suppose that a sum of $1,000 is invested for two years at an annual rate of interest of 8%. What is the future value of this sum based on the following compounding frequencies?
- Annual compounding
- Semi-annual compounding
- Monthly compounding
With annual compounding, t = 2, r = 8% and PV = $1,000.
FVt = PV*(1+r)^t
FV2 = 1,000*(1+.08)^2
FV2 = 1,000*(1.16640)
FV2 = $1,166.40
With semi-annual compounding, t = 4, r = 4% and PV = $1,000. The time frame is now 4 semi-annual periods, and the rate of interest is 4% per semi-annual period.
FVt = PV*(1+r)^t
FV4 = 1,000*(1+.04)^4
FV4 = 1,000*(1.16986)
FV4 = $1,169.86
With monthly compounding, t = 24, r = 0.6667% and PV = $1,000.
FVt = PV*(1+r)^t
FV24 = 1,000*(1+.006667)^24
FV24 = 1,000*(1.17289)
FV24 = $1,172.89
These results show that the future value of a sum continues to increase as the compounding frequency increases.
For the present value, a higher compounding frequency reduces the present value. This is because more compound interest is earned, which reduces the amount that must be saved today to be worth a specified sum in the future.
As an example, suppose that an investor has a target of $100,000 in five years, and can invest in a bank account that pays an annual rate of interest of 6%. How much must the investor save today in order to reach this goal based on the following compounding frequencies?
- Annual compounding
- Semi-annual compounding
- Monthly compounding
With annual compounding, t = 5, r = 6% and FV5 = $100,000.
PV = FVt / (1+r)^t
PV = 100,000 / (1+.06)^5
PV = 100,000 / 1.33823
PV = $74,725.82
With semi-annual compounding, t = 10, r = 3% and FV10 = $100,000.
PV = FVt / (1+r)^t
PV = 100,000 / (1+.03)^10
PV = 100,000 / 1.34392
PV = $74,409.39
With monthly compounding, t = 60, r = 0.5% and FV60 = $100,000.
PV = FVt / (1+r)^t
PV = 100,000 / (1+.005)^60
PV = 100,000 / 1.34885
PV = $74,137.22 (Article Index)
7) Annuities
An annuity is a periodic stream of equally-sized payments. The word annuity is derived from the Latin word annum (yearly). In spite of this, any stream of periodic payments of equal size can be treated as an annuity. As an example, mortgage payments are made monthly and are of equal size, and so can be thought of as a type of annuity.
The two basic types of annuities are:
- Ordinary annuity
- Annuity due
Ordinary Annuities
With an ordinary annuity, the first payment takes place one period in the future. Most annuities are ordinary; some examples are:
- Coupons paid by a bond
- Dividend payments by a share of preferred stock
- Car loan payments
- Mortgage payments
- Student loan payments
- Social security payments
The Future Value of an Ordinary Annuity
The formula for computing the future value of an ordinary annuity is:
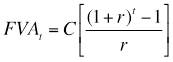
where:
FVAt = future value of a t-period annuity
C = the periodic cash flow
r = periodic interest rate
t = number of periods until the sum is received
As an example, suppose that a sum of $1,000 is invested each year for four years, starting next year, at an annual rate of interest of 3%. Since the cash flows start next year, this is an ordinary annuity. What is its future value? In this case, t = 4, r = 3% and C = $1,000.
Alternatively, the future value of each individual cash flow can be computed and then combined as follows:
The first cash flow is invested for three years (from year one to year four):
FV3 = PV(1+r)t
FV3 = 1,000(1+.03)3
FV3 = 1,000(1.09273)
FV3 = $1,092.73
The second cash flow is invested for two years (from year two to year four):
FV2 = PV(1+r)t
FV2 = 1,000(1+.03)2
FV2 = 1,000(1.06090)
FV2 = $1,060.90
The third cash flow is invested for one year (from year three to year four):
FV1 = PV(1+r)t
FV1 = 1,000(1+.03)1
FV1 = 1,000(1.03)
FV1 = $1,030.00
The fourth and final cash flow does not earn any interest since it is not deposited into the bank until year four. The future value is therefore $1,000.
The sum of these future values is:
$1,092.73 + $1,060.90 + $1,030.00 + $1,000.00 = $4,183.63
The Present Value of an Ordinary Annuity
The formula for computing the present value of an ordinary annuity is:
where:
PVAt = present value of a t-period ordinary annuity
C = the value of the periodic cash flow
As an example, how much must be invested today in a bank account that pays 5% interest per year in order to generate a stream of payments of $1,000 in each of the following three years? In this case, t = 3, r = 5% and C = $1,000.
Alternatively, the present value of each individual cash flow can be computed and then combined as follows:
The present value of the first cash flow (paid in one year) is:
PV = FVt / (1+r)t
PV = 1,000 / (1+.05)1
PV = 1,000 / 1.05
PV = $952.38
The present value of the second cash flow (paid in two years) is:
PV = FVt / (1+r)t
PV = 1,000 / (1+.05)2
PV = 1,000 / 1.10250
PV = $907.03
The present value of the third cash flow (paid in three years) is:
PV = FVt / (1+r)t
PV = 1,000 / (1+.05)3
PV = 1,000 / 1.15763
PV = $863.84
The sum of these present values is:
$952.38 + $907.03 + $863.84 = $2,723.25
Annuities Due
With an annuity due, the first payment takes place immediately. This is a less common type of annuity than the ordinary annuity. An example of this would be a lease agreement or a loan where the first payment is due immediately.
Due to the timing of the cash flows, the present value and future value of an annuity will be affected by whether the annuity is an ordinary annuity or an annuity due.
The Future Value of an Annuity Due
The future value of an annuity due is computed as follows:
FVAdue = FVA ordinary * (1+r)
This shows that the future value of an annuity due is greater than the future value of an ordinary annuity. This is because each cash flow of an annuity due is invested for one additional year.
Referring to the previous example, the future value of an annuity due would be: 4,183.63(1+.03) = $4,309.14
This can be confirmed by computing the future value of each cash flow individually. Each cash flow will be invested for one additional year compared with the ordinary annuity.
The first cash flow is invested for four years (from today to year four):
FV4 = PV(1+r)t
FV4 = 1,000(1+.03)4
FV4 = 1,000(1.12551)
FV4 = $1,125.51
The second cash flow is invested for three years (from year one to year four):
FV3 = PV(1+r)t
FV3 = 1,000(1+.03)3
FV3 = 1,000(1.09273)
FV3 = $1,092.73
The third cash flow is invested for two years (from year two to year four):
FV2 = PV(1+r)t
FV2 = 1,000(1+.03)2
FV2 = 1,000(1.06090)
FV2 = $1,060.90
The fourth cash flow is invested for one year (from year three to year four):
FV3 = PV(1+r)t
FV3 = 1,000(1+.03)1
FV3 = 1,000(1.03)
FV3 = $1,030.00
The sum of these future values is:
$1,125.51 + $1,092.73 + $1,060.90 + $1,030.00 = $4,309.14
The Present Value of an Annuity Due
The present value of an annuity due is computed as follows:
PVA due = PVA ordinary * (1+r)
This shows that the present value of an annuity due is greater than the present value of an ordinary annuity. This is because each cash flow of an annuity due is paid one year sooner, so that the invested principal earns less interest. As a result, a larger sum must be invested in order to generate the appropriate cash flows.
Referring to the previous example, the present value of an annuity due would be: 2,723.25(1+.05) = $2,859.41
Alternatively, the present value of each individual cash flow can be computed and then combined as follows:
The first cash flow is withdrawn immediately, so the present value equals $1,000.
The present value of the second cash flow (paid in one year) is:
PV = FVt / (1+r)t
PV = 1,000 / (1+.05)1
PV = 1,000 / 1.05
PV = $952.38
The present value of the third cash flow (paid in two years) is:
PV = FVt / (1+r)t
PV = 1,000 / (1+.05)2
PV = 1,000 / 1.10250
PV = $907.03
The sum of these present values is:
$1,000 + $952.38 + $907.03 = $2,859.41 (Article Index)
8) Perpetuities
A perpetuity is an investment in which interest payments are made forever, but principal is not repaid. As an example, a stock that pays a regular stream of constant dividends can be thought of as a perpetuity. This is because the same cash flows are paid each year, and the stock has an infinite lifetime. Another example is a consol, which is a bond that makes interest payments forever but does not repay the principal.
The Present Value of a Perpetuity
The present value of a perpetuity that pays an annual cash flow of $C per period is:
PV = C/r
As an example, suppose that a perpetuity pays $100 per year; assume that the appropriate rate of interest is 5% per year. The present value of the perpetuity is $100/0.05 = $2,000.
The Present Value of a Growing Perpetuity
Suppose that the cash flows provided by a perpetuity grow at a fixed rate each year. The present value formula is adjusted as follows:
PV = C/(r – g)
where:
g = annual growth rate of the perpetuity
As an example, suppose that a perpetuity currently pays $50 per year; assume that the appropriate rate of interest is 7% per year, and that the cash flow paid by the perpetuity is estimated to grow at a rate of 3% per year. The present value of the perpetuity is: $50/(0.07 – 0.03) = $1,250. (Article Index)
9) Interest Rate Conventions
Interest rates for loans, bank accounts, etc. can be quoted in two basic ways:
- Annual percentage rate (APR)
- Effective annual rate (EAR)
The annual percentage rate reflects the simple interest of a loan or an investment, while the effective annual rate reflects both the simple and compound interest.
Converting APR to EAR
In order to compare interest rates with different compounding frequencies, they can be converted into an effective annual rate (EAR); this reflects the true cost of borrowing (or the return to lending) when interest is compounded more than once per year. EAR is computed from APR as follows:
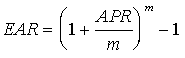
where:
m = the number of compounding periods per year
As an example, suppose that a bank charges an APR of 6% per year, compounded quarterly for a loan, what is the effective annual rate? This can be determined as follows:
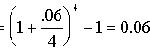
This indicates that the borrower is actually paying 6.136% per year for this loan.
Converting EAR to APR
An effective annual rate may be converted to an annual percentage rate by inverting the previous formula:
As an example, if a bank charges an EAR of 5.25% per year, compounded monthly for a loan, what is the annual percentage rate? This can be determined as follows:
10) Continuous Compounding
Continuous compounding is the limit of compounding frequency. Continuous compounding indicates that interest rates are being compounded at every instant in time, which implies that interest is compounded an infinite number of times. A compounding frequency which is not continuous is said to be discrete. For example, annual compounding, monthly compounding, daily compounding, etc. are all examples of discrete compounding.
Using continuous compounding requires a new set of formulas for computing the future value of a sum, the present value of a sum, EAR and APR.
Computing the Future Value of a Sum with Continuous Compounding
If interest rates are compounded continuously, the future value of a sum is:
FVt = PV*(e^rt)
where:
e is a constant that is approximately equal to 2.71828
As an example, suppose that a bank offers a rate of interest of 6%, compounded continuously. An investor who deposits $1,000 in this bank for two years will have an ending balance of: FVt = 1,000(e(0.06)(2)) = $1,127.50
Computing the Present Value of a Sum with Continuous Compounding
The present value of a sum with continuous compounding is:
PV = FVt*(e^-rt)
As an example, suppose that a bank offers a rate of interest of 8%, compounded continuously. An investor who needs to have $10,000 in three years will have to save the following amount today in order to reach this goal: PV = 10,000(e^-(0.08)(3)) = $7,866.28
Computing EAR with Continuous Compounding
If interest rates are compounded continuously, EAR is computed as follows:
EAR = eAPR – 1
As an example, if a bank charges an APR of 4% per year, what is the EAR with continuous compounding?
EAR = e^APR – 1
= e^0.04 – 1
= 1.04081 – 1
= 0.04081 = 4.081%
Computing APR with Continuous Compounding
If interest rates are compounded continuously, APR is computed as follows:
APR = ln*(1 + EAR)
As an example, if a bank charges an EAR of 3.5% per year with continuous compounding, what is the APR?
APR = ln*(1 + EAR)
= ln(1.035)
= 0.03440
= 3.440% (Article Index)
Next Steps: Now that you have a good understanding of what the time value of money is and the associated concepts, why not continue to read related topics? You can either proceed to learn more about:
- Fixed Income Securities; which includes:
- How to read financial statements; which includes:
- Learning how to read a balance sheet; or
- Learning how to read a cash flow statement; or
- Learning how to understand and interpret percentage statements.
If you have more questions on the time value of money, feel free to call our accounting or finance teams and we will be happy to assist you.