Linear Programming using Solver: Tutoring and Top Tips

Operations are an essential and integral part of every business. So, every business student encounters an operations management course early in his or her MBA program. And every operations management course will contain linear programming tutorials. The depth and breadth of linear programming tutored may vary among courses, but every MBA program will expect students to be familiar with the essential linear programming (LP) concepts and Microsoft Excel’s solver function.

Some operations management programs only expected students to know the underlying LP theory and interpret solver linear programming sensitivity reports and answer reports. However, most operations management programs expect MBA students to tackle a variety of linear programming settings using Microsoft Excel’s solver function including transportation, scheduling, optimization, multi-period cash flows, investment decisions, and more. While most MBA programs use Microsoft Excel’s solver to tackle linear programming problems, some operations management courses also introduce students to specialized LP software.

Tutoring LP with Solved Examples

Optimization and linear programming are challenging for most students. We find it easier to teach optimization and linear programming using LP examples. Let’s take an example to illustrate how you can tackle a LP question.

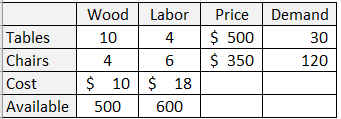
Let’s assume you are the owner of a small furniture-making factory that only makes tables and chairs. The inputs required to make tables and chairs are wood and labor. Let’s assume that each table requires 10 units of wood and 4 hours of labor and each chair requires 4 units of wood and 6 hours of labor. Each unit of wood costs $10 and each hour of labor costs $18. We know that tables sell for $500 and chairs sell for $350 and estimate that there is a demand for 30 tables and 120 chairs this week. We also know that we have 500 units of wood and 600 hours of labor time. You need to decide how many tables and chairs to produce this week? How will you make your decision?

Please take a few minutes here to write down an answer. Can you see this as a LP problem? We will then proceed with this solved LP example as an illustration of the steps we recommend to tackle LP problems using Microsoft Excel’s solver functions.

LP Solver Structure

You have to break down the question or challenge into three components when tackling linear programming problems. The objective function, the decision variables and the constraints. Microsoft Excel’s solver is built on these three LP components.

The Objective Function in LP Solver

The objective function is what you as a decision-maker is trying to maximize or minimize. The objective function is a single metric used to evaluate the success of your decisions and outcomes. In our example, you will be seeking to maximize the profits as a business owner. Often the word optimize is used. You may maximize revenues or traffic or maybe minimizing costs in many LP problems. You are most interested in profits and so maximizing profits becomes the objective function in our LP problem.

The Decision Variables in LP Problems

The decision variables are the things (LP variables) you can control. To identify the decision variables, ask yourself the questions: What can I change? Or what can I control? In our LP problem, you cannot change the demand for tables or decide to build a table with only three legs to reduce the amount of wood needed nor can you pay your labor a lower wage. But what you can decide on is the number of tables and chairs you will make! So the number of tables and chairs you will make become your decision variables. LP problem will indicate what you deciding on directly or indirectly.

The Constraints in an LP Problem

Resources and inputs are limited. Constraints are the resources or inputs that limit you. You can increase profits by increasing the number of tables and chairs infinitely! However, there is a limit on the amount of wood and labor you have. So, these are constraints in your LP problem. You cannot sell an unlimited number of tables and chairs. Therefore, the number of chairs and tables you can sell in a week also becomes a constraint in your LP problem! Two common constraints that are no obvious in questions are 1) the decision variables cannot be negative and 2) decision variables are integers. (Binary and integer linear programing are more specific topics and not covered here). Also check for other upper and lower bounds on your decision variables.

You must break down all linear programming problems into these three components: the objective function, the decision variables and the constraints. You cannot proceed to solving or optimizing a linear programming problem without defining the objective function, the decision variables, and the constraints.

Describing an LP Problem

Once you understand your linear programming problem, you can describe the objective function, the decision variables and the constraints in three ways. You can describe the objective function, the decision variables, and the constraints:

1. In English;
2. Algebra; and
3. In a Microsoft Excel model.

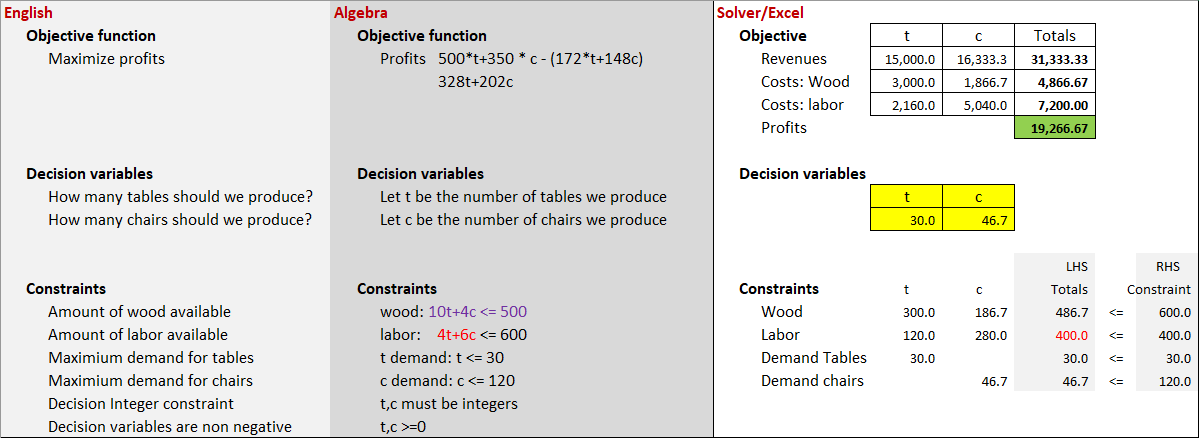
Some operations management professors would like you to learn how to describe an LP problem using only one or two approaches. Our graduate operations management tutors encourage MBA students to be proficient in describing LP solver’s components the objective function, the decision variables and the constraints using all three approaches.

Steps in Building a LP model in Microsoft Excel

1. A clear step-by-step process to solve linear programming problems using Microsoft Excel’s solver makes it easier for MBA students. Here are the steps we recommend to solve an LP problem.
2. Read the problem to the end including the sub-questions.
3. Transcribe the quantitative aspects of the problem in Excel. This step helps you identify the quantitative data that become the LP problem’s solver inputs.
4. Describe the LP problem using the objective function, decision variables and constraints. You can describe the linear programming problem’s objective function, the decision variables, and the constraints in English, algebraically or in a Microsoft Excel model.
5. Set up the decision variables in empty cells with their titles in adjacent cells. I usually color it yellow to make it stand out. Assume you will have 1 in each of these decision variables to start.
6. Build out the objective function in a cell and highlight it in green. The objective function computation must have no hardcoded input and must be a function of the decision variables.
7. Build out the constraints cells.
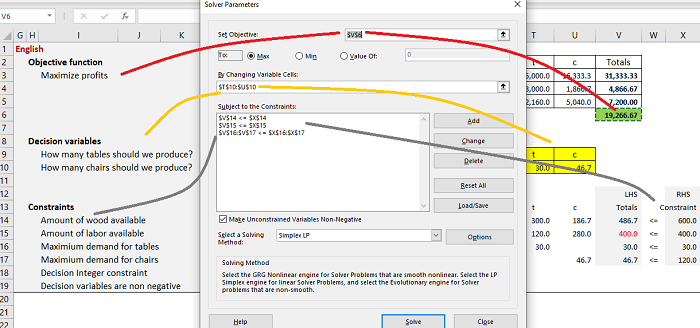
8. Set up Microsoft Excel’s solver. Fill out the objective function, decision variables and constraints.
9. Run Microsoft Excel’s solver.
10. Check if the constraints are met. If the constraints are not met, go back to the solver wizard and check if you have entered the objective function, decision variables and constraints correctly. You may have also missed entering a constraint or forgotten to check the “make unconstraint variables non-negative” box.
11. Evaluate the answer report, sensitivity report and limits report.

Top 5 LP Solver tips that helped our MBA students

1. Transcribe the quantitative aspects of the problem in Excel before building the LP Solver Model.
2. Avoid any hard coded formula cells when building the LP Solver model’s objective function and constraint cells.
3. Build the LP model with 1 in each of these decision variables to start.
4. Please the LHS of the constraint equations and RHS of the constraint equations next to each other.
5. Color code the objective function cell in green, decision variable cells in yellow and constraint cells in grey to identify them clearly when filling out the LP Solver function.

Follow the LP problem solving steps and top 5 LP tips to crack your LP problems. Do email or call us if we can help you with LP tutoring.

LP Practice Problem

Should you want to try your hand solving an LP Problem, you have one below.

You manager has asked you to decide how many TV and Newspaper ads to run for the coming Christmas season. Every TV ad costs $40,000 and each NP ad costs $25,000. Every TV ad will reach 1 million people and each NP ad will reach 2 million. You have a budget of $300,000 which you allocated between TV and NP. You manager wants to ensure you spend less than $180,000 on NP ads given readership profiles.

Enjoy Linear Programming!

Operations Research Tutoring

Our operations research tutors can assist you with tutoring for linear programing using Microsoft’s Solver.  Other operations topics we can assist you include queuing theory and waiting lines, decision trees, linear programing using Microsoft Excel’s Solver, newsvendor models, batch processing, Littlefield simulation games. etc. Feel free to call or email if we can be of assistance with live one on one tutoring.